Newton’s First Law
This law is sometimes called the law of inertia. It essentially says that an object will maintain constant velocity unless influenced by an unbalanced force.
Sometimes you may hear the principle divided into two possibilities. Those being “at rest” or “moving in a straight line.” As discussed before, a vector quantity has both magnitude and direction and velocity is a vector quantity. An object at rest simply has a (constant) velocity of zero and an object moving in a straight line has a velocity with unchanging, constant magnitude and direction. Therefore these two can be summarized into one as simply “constant velocity.”
The “unbalanced force” qualification is added since it is possible to have multiple applied forces that cancel each other out and consequently have no effect on the velocity of the object. Consider a stationary ball that I push on two opposite sides, and I push in exactly opposite directions along the same line of action. I may compress or squish the ball, but if the two forces are of equal magnitude and in opposite directions, the ball as a body will not move.
Newton’s Second Law
The second law shows how the velocity (more precisely the momentum) will change when an unbalanced force is applied. This law which is often shown in this form:
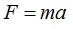
Is actually more fully described by:
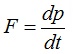
This says that the total (unbalanced) force applied to the object will be equal to the instantaneous change in linear momentum (p) per unit time, and linear momentum (vector) is the product of the mass (scalar) and the velocity (vector). If we assume the mass stays constant (true for thrown balls, but not for rockets whose mass diminishes as the fuel is used up) then we arrive at the typical representation shown above:
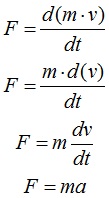
Newton’s Third Law
The third law says that for every action (applied force) there is an equal and opposite reaction (reactionary force). When I push a car, the car also pushes on me. You might say, “The car isn’t really pushing on me.” This is true in an initiating or active sense, but not completely. Typically if I stand and push on a car, neither I nor the car moves. This is because of the friction force with the ground. This does not mean there are no forces. In other words, like the example above with the ball and the first law, the total unbalanced force is zero. The various forces cancel out essentially and there is no change in the (zero) velocity of either object. But if I stand on a skateboard and push on the car then I will move away from the car. This is because of the reactionary force applied to me from the car. Going further, if I stand on a skateboard and I put the car in neutral (and I am pushing along the longitudinal axis of the car), I will move away from the car and the car will move away from me. The total unbalanced force on the car and the car’s unbalanced reactionary force on me both result in a change in linear momentum (really a change in velocity or acceleration since our mass has not changed) according to the second law.